Годинник | |
|
Решение задачи 1c
|
| |
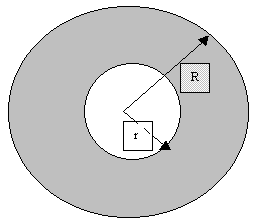
Обозначим радиус и массу Земли соответственно R и M. Допустим тело находится на расстоянии r<R от центра Земли. Область от r до R на рисунке заштрихована. Легко доказать, мысленно разбивая внутреннюю поверхность заштрихованной сферической оболочки на множество малых элементов, что на тело внутри этой области со стороны внешних областей сила тяготенине действует.
Таким образом, на тело в шахте действует сила притяжения от части Земли с радиусом r и массой m=M*(r/R)3. Учитывая данное обстоятельство, получим для силы притяжения в шахте F=m*g*r/R. Для ускорения в шахте получим выражение: a=g*r/R или вводя обозначение g/R=w2 имеем a=w2*r. Мы получили уравнение для колебательного движения с периодом T=2*p*SQR(R/g). В самом деле движение тело в шахте будет иметь колебательный характер: оно проскочит центр Земли, дойдёт до поверхности в противоположной стороне, повернёт обратно к центру и т.д.
Данные рассуждения справедливы, если не принимать во внимание неоднородность плотности Земли.
Искомавеличина t=T/4=(p/2)*SQR(R/g).
|
|
|
|
|